The Kruskal-Wallis H-test is a non-parametric statistical method used to determine whether three or more independent groups originate from the same distribution. As the non-parametric alternative to one-way ANOVA, it’s particularly valuable when data violates normality assumptions or when working with ordinal variables.
Unlike parametric ANOVA that compares group means, the Kruskal-Wallis test evaluates differences in median ranks across groups. This makes it good for:
Common applications include clinical trials comparing multiple treatments, customer satisfaction surveys across regions, or any scenario comparing ≥3 independent groups with non-parametric data.
The Kruskal-Wallis test returns two key numbers:
This is how you see the Kruskal-Wallis results with SimpliStats
Important Note: A significant result doesn’t indicate which groups differ – post hoc tests are needed for pairwise comparisons.
Suppose you compare customer satisfaction scores (1-10 scale) across three store locations:
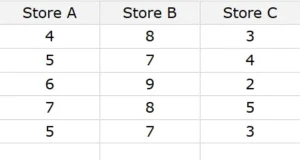
Since 0.0039 < 0.05, you conclude:
“There are statistically significant differences in satisfaction scores between at least two store locations.”
from scipy.stats import kruskal
statistic, pvalue = kruskal(group1, group2, group3)
Input
Output
The Kruskal-Wallis test is a robust non-parametric method for comparing multiple independent groups. While it identifies whether differences exist, researchers should plan for post hoc tests to pinpoint specific group disparities. Its flexibility with non-normal data and unequal sample sizes makes it invaluable across scientific, business, and social research contexts.
SimpliStats | 2025 © All rights reserved – Privacy Policy | Terms and Conditions